The physics of my foam rocket
 Introduction
Introduction
I got a small foam rocket for Christmas. It works as follows, you use a pump to
pressurise a small base unit. The base unit has a rod onto which you slide the
foam rocket It has a small pressure gauge which gives a rough estimate of how
high the foam rocket will go. Once you've supplied the desired amount of
pressure, you press a small release button that fires the rocket using the air
you've compressed. At full pressure, the rocket flies to around 120 feet into
the air.
Being Simon, I asked myself two questions:
- How fast is the rocket going when it leaves the stand?
- What is the average acceleration of the rocket before it leaves the stand?
This is elementary physics problem, however, if we just produced the correct equations, as if by magic, it wouldn't be much of an article so to make this more article worthy, we're going to do the whole thing from first principles, like only Simon would.
A discussion of Work
My laptop, on which i'm writing this article, has two forces acting on it. The
force of gravity pulling the laptop down to the table and the electromagnetic
repulsion between the electrons on bottom of my laptop and the table
preventing it falling any further. These forces are in an exact balance so
there is no overall acceleration of my laptop.
So there must be a distinction between a force that is doing an acceleration and one that isn't. This distinction is called "Work". Work is defined as the integral of the dot product of the force and the distance over which that force was applied.
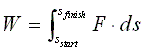
Figure 1.1 - Definition of Work.
We're going to use Newton's theory of gravity here (the error introduced by doing so is tiny compared to the other errors in our estimation) so we can consider gravity to be a force. Since this force operates over a distance (namely, the height the rocket flies) then we must conclude work is done on the rocket throughout the flight.
To get our desired results from first principles, we need to do two things. First, calculate the work done on the rocket by gravity and second, show that the work required to stop a body in motion depends only on the mass and velocity of that body and to derive an equation that relates work to these two properties.
The work done on the rocket by Gravity
Newton postulated that gravity was a force and that the size of this force depended only on the mass of the two bodies and their separation. Put mathematically, if F is the magnitude of the force, r is the separation and M and m are the masses of the two objects involved then:
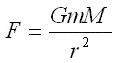
Figure 1.2 Newton's law of Gravity
Where G is a fixed constant, called the gravitional constant. The distance r is the length of the line that connects the centre of masses of the bodies. In our case, we want to compare the strength of the force between a the ground and about 48 meters above the ground. Using the following numbers:
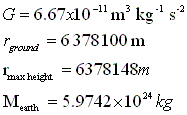
Figure 1.3 Values required for our calcuation
From our definition of work in Figure 1.1 we now have enough data to calculate the work done by gravity on the rocket by the time it stops at it's peak height. We deliberately omit the mass of the rocket from the integral below because we will see that we don't need to know that value in order to solve our problem:
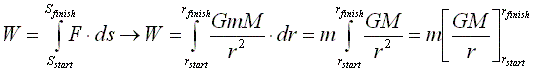
Figure 1.4 Solving the integral
Now it's just a question of putting in the numbers:
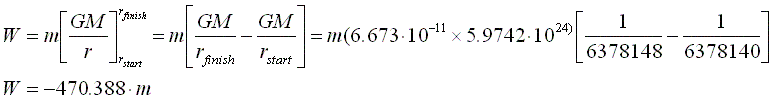
Figure 1.5 Putting in the numbers
The minus sign might worry you but it's okay. Gravity always decelerates a body and work is defined as a force accelerating a body through a distance so the minus sign naturally comes out of our equation since we're decelerating. We'll revisit Figure 1.5 later.
Finding an expression for the Work done in terms of Mass and
speed.
In figure 1.1 the definition of Work is given as the integral of the dot
product of the Force and the distance over which that force is applied.
Intuition tells us that if a force acts over a distance on a body then that
body ought to accelerate and it is harder to accelerate a large body than it is
to accelerate a light body. It should, therefore, be possible to find the
amount of work required to accelerate a body to a speed, v, using only the mass
of the body and that speed.
Let's examine our definition of Work again:
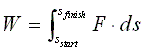
Figure 1.1 Definition of Work
Newton's second law is a Force accelerating a body is defined as the rate of change of momentum of that body:
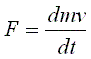
Figure 1.6 Newton's Second Law
In almost all cases the mass in a system is kept constant. So Figure 1.6 becomes:
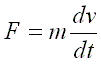
Figure 1.7 Newton's Second Law for Constant Mass
Next, we substitute Figure 1.7 into our definition of Work:
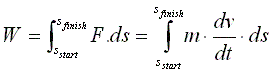
Figure 1.8 Substituting Fig 1.7 into Fig 1.1
Now we do some rearrangement:
Figure 1.9 Rearrange and Manipulate Fig 1.8
This step might be a little confusing so i'll go through it. Fig 1.7 shows dv
by dt multiplied by ds. What Figure 1.9 shows is that we can write this as (dv
times ds) by dt. We can then take dv outside to give (ds by dt) multiplied by
dv. ds by dt which is clearly the rate of change of distance which is v. So we
can write v multiplied by dv in the integral. It looks like a bit of witch
craft but we can get away with it.. ![]()
For our problem, we want to consider the work done in accelerating a body from speed 0 to some speed Vfinal. So we solve Figure 1.8 with vstart=0:
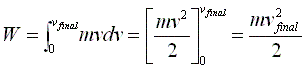
Figure 1.10 Obtaining the Kinetic energy equation
It's clear that Figure 1.10 is an equation relating Work require to accelerate an object to speed Vfinal is dependant on only that speed and the mass of the body - exactly the point we wanted to derive.
Putting it all together
My first goal for this article was to determine, from first principles, how fast
the foam rocket leaves the stand. With Figure 1.10 and 1.5 we are now in a
position where we can determine this.
Figure 1.5 tells us the amount of work done on the rocket by gravity over the 48 meter height that the rocket climbs too. The secret to cracking this problem is realising at the top of the 48 meter climb, the rocket momentarily stops. Gravity is working on the body right from the moment it leaves the stand so all the energy to climb all 48 meters must come from the initial speed the body carries.
To see this, imagine for a moment we could make time run backwards. We'd see the rocket start at 48 meters above the ground and accelerate to the ground. The speed the body is just before it leaves the stand would be equal to the amount of work done by gravity over the 48 meters. This allows us to determine the speed when it left the stand by equating Fig 1.10 and 1.5*:
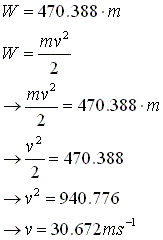
Figure 1.11 Deriving the muzzle velocity
30.672 meters a second translates to 110.419 kilometers per hour or 68.611 miles per hour. Quite fast, I think you'll agree.
The next thing to tackle is the acceleration of the rocket as it leaves it's stand. The acceleration we calculate here is an average since the way the acceleration actually happens as a function of the height up the stand is probably very complicated. For our argument, we assume that the rocket accelerates at a constant rate.
Once again, we bring out our trusty definition of work:
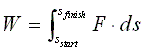
Figure 1.1 Definition of Work
Combine this with our definition of a force in Figure 1.6 then we get:
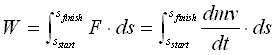
Figure 1.12 Combination of Figure 1.1 and 1.6
Since the mass of our rocket is constant and we're assuming that the acceleration, a=dv by dt, is also a constant then the integral above simplifies to:
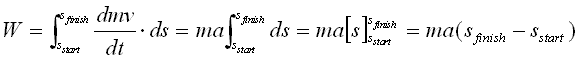
Figure 1.13 Obtaining a formula for work done under constant acceleration
If we define the bottom of the stand to be zero and Sstart, then Figure 1.13 becomes masfinish. The work done that we've derived here is must be equal to work done in accelerating the rocket from rest to it's take-off velocity. So equating Figure 1.10 with this result we obtain a formula for the average acceleration experienced by the rocket:
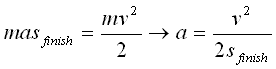
Figure 1.14 Equation Figure 1.10 and Figure 1.13 for Sstart = 0
The stand is roughly 0.2 Metres long so all that is left to do is to put in the numbers and out comes the answer:
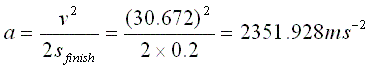
Figure 1.15 Putting in the numbers.
That might sound like a huge number for a little foam rocket but it's actually quite reasonable when you consider it does 0-60mph in 0.2 meters. Put another way, if you were accelerated that much you'd momentarily weigh 240 times what you do normally. Quite remarkable!.
The analysis in this article is approximate. It neglects all frictional forces and doesn't make exact measurements of the height attained by the rocket
or the length of the stand.. Also, the jet of air might continue to accelerate the body once it leaves the stand. This said, it's reasonably good estimate of
the speed and acceleration of the rocket and it derives the mechanics from first principles so
i'm quite proud of the article. One day, I might do a follow up with a more exact analysis! If you've got this far, then thanks for reading and have a nice day. ![]()
Simon
Copyright Simon Johnson 2004