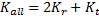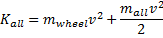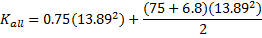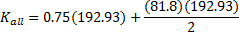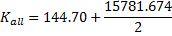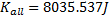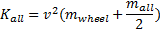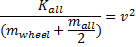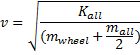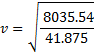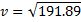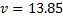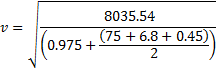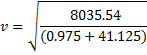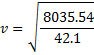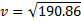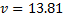Does one pound on the wheels equal two pounds on the frame?
Introduction
There is an adage that each pound added to the wheels is equal to two added in the frame.
But is this really true?
The approach
The approach taken in this post is to create a control bicycle (with no mass added) and then two bicycles with the same mass added but with one bike having it all on the wheels and the other having it all on the frame.
Before we go any further, we need to understand the basic energy equation of a bicycle. This model is rather simple in that it just looks at the energy of the system rather than the action under frictional forces such rolling resistance and the friction of moving through the air. However, this is not really a limitation of the approach; if the two bikes under consideration are identical in every other respect and the rider is the same mass and rides in the same position - then these effects can be safely ignored.
Modelling the bicycle
At its most basic, a bicycle is a system with two stores of energy. One store is the translational energy of the bicycle that is stored in its forward movement. The other is the rotational energy of the bicycle that is stored in the rotation of its wheels. The energy equation of a bicycle is simply the sum of these two components.
The translational stored in the bicycle is straightforward enough:
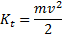Fig 1.1 - Kinetic energy equation
The rotational energy stored within the wheels can be computed using an equation of a similar form:
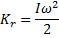Fig 1.2 - Rotational energy equation
The I parameter represents the rate of rotation of the wheel. The I parameter represents the “difficulty” of changing the rate of rotation of the wheel; it’s called the “moment of inertia.”
This changes depending on the shape of the object and can be quite tricky to compute. Fortunately, Wikipedia has already done the hardwork for us and gives the following equation for a wheel:
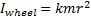Fig 1.3 - Moment of inertia for a wheel
Where m is the mass of the wheel and r is its radius. For a bicycle wheel, k is known to be 1. We can substitute this in to the rotational energy equation to give us the rotational energy equation for a wheel:
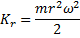Fig 1.4 - Rotational energy equation for a wheel
We can rework this equation to remove the omega parameter and instead work in terms of the tangential speed of the wheel. This is done by substituting v squared over r for I:
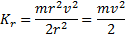Fig 1.5 - Rotational energy for a wheel, written in terms of *v*
Here, the v parameter is the tangential speed of the wheel. If you imagine swinging a nut tied to a piece of string in a circle, the length of the string is equal to the radius of the wheel and the rate of rotation is equal to Ï. If it were suddenly released, v is the speed it would shoot off in any particular direction.
Now we can write the energy equation for the whole bicycle:
That is to say, the total energy of the system is the kinetic energy summed with the rotational energy of both wheels.
We can see immediately that the adage is true. If a pound is added to the wheels, it is counted twice. Once in the energy equation for the wheels and again in the kinetic energy equation for the whole bike.
However, how much of an affect this has in a practical sense can be illustrated by working a few examples.
The control
Lance Armstrong has a mass of 75 kilograms. Let’s assume that the bicycle has mass of 6.9 kilograms. That’s one hundred grams over the UCI-mandated 6.8 kilogram limit. Let’s further assume that each wheel in the control has a mass of 0.75 kilograms.
If Lance is doing 50 kilometres an hour, or 13.89 meters per second, then his total energy is:
A pound on the frame
We start by looking at the effect of adding a single pound to the frame. A pound is 0.45 kilograms and it is a relatively small mass compared to the mass of Lance plus the bike.
Nonetheless we shall we how fast he can go using the 8035.54J of energy on this bicycle.
To do this, we first need to make v the subject of the energy equation. This is relatively straightforward:
Now we just plug in the numbers:
That’s 49.86 kilometres per hour. That’s a difference of 0.14 kilometres per hour over the base set-up and a difference of about 1% overall.
A pound on the wheels
There are two wheels each having a mass of 0.75 kilograms. If we add half a pound to each wheel then we get 0.975 kilograms per wheel.
Plugging this in to the equation derived in figure 3.1, we get:
That’s 49.72 kilometres per hour. That’s a difference of 0.29 kilometres per hour or 2% on the control. As you can see, this confirms the result we expected from just looking at the equation. Adding a pound to the wheels really is equivalent to adding two to the frame.
Conclusion
So the adage is true! Adding a pound to the wheels is like adding two pounds to the frame.
The reason is that the mass has to be both accelerated in the direction of travel and rotated around the wheel; the extra mass affects both mass variables in the equation.
However, like all things mass related in biking, unless you’re Lance Armstrong fighting for the top spot in the Tour De France you probably shouldn’t concern yourself with this too much. Even with the very lightest road bike you can possibly race, the difference is only a few percent. On your typical road bike, it’s going to be even less.
Happy cycling!