How wings produce lift
Many of us think we know how wings produce lift. The explanation we’re taught in school works something like this:
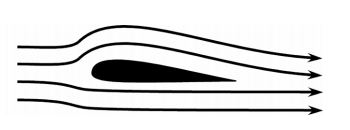
The air moves in from the left and exits the scene behind the wing.
- If we trace a streamline across the bottom of the wing the air covers a certain distance.
- If we trace a streamline across the top of the wing, the air covers a larger distance.
- The air takes an equal amount of time to traverse the two streamlines.
- Therefore, the air following the streamline across the top of the wing moves more quickly than the air below the wing.
- By Bernoulli’s equation, the air pressure above the top of the wing is lower than the bottom.
- This difference in pressure produces lift.
This is completely incorrect. The most straightforward way to see this is through the following picture:

According to the argument given above, the geometry of the wing is crucial to generating lift. If that’s the case, then surely it should be impossible for a plane to maintain altitude while flying upside down?
With a little more thought, we can see that the theory of lift given above also predicts that the wing should generate that maximum amount of lift at precisely zero degrees to the incident airflow. This is because the lifting force comes from the difference in pressure from the lower slipstream to the upper slipstream and this is created by the geometry of the wing.
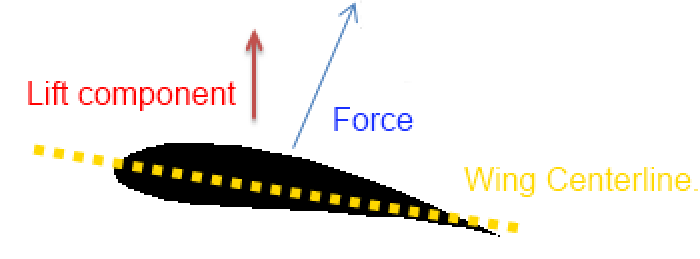
The force would always be at 90 degrees to the line going through the centre of the wing. This means that when a wing is presented to the air flow at an angle (called the angle of attack) the lift is lower that it being presented to the air with no angle. This is the precise opposite of what is observed:

The reason planes roll to this attitude during take-off is precisely because more lift is generated by increased angle of attack, not less.
Finally, there is a no evidence to support the assertion “The air takes an equal amount of time to traverse the two streamlines.” In fact, as you’ve probably guessed by now, the opposite is true. The air traverses the top part of the wing faster than the bottom.
Newtonian Lift
Now that we’ve debunked the common model of lift, we now need a working replacement.
All that’s needed is for us to recap on Newton’s laws:
- First Law: - The velocity of a body remains constant unless the body is acted upon by an external force.
- Second Law: - The acceleration a of a body is parallel and directly proportional to the net force F and inversely proportional to the mass m, i.e., F = ma.
- Third Law: - To every action there is always an equal and opposite reaction: or the forces of two bodies on each other are always equal and are directed in opposite directions.
By deduction we can bring the picture in to focus. If there is a force upwards, there must be an equal and opposite reaction downwards. Given this, it is almost obvious that the wings must be deflecting air downwards.

The next question is how the wings do this? The first thing to appreciate is that air is a fluid and it has a viscosity.
If you look at this picture of this stream, you’ll see that the flow in the middle of the stream is running more quickly than at the banks. You can see this by the “dragging” effect in the water flow.

If we were to measure the velocity of the water right at the edge of the bank, we’d find the velocity to be precisely zero. As we move further and further in to the middle of the stream the velocity would slowly increase to the flow rate for the stream.
A wing works the same way. The air in contact with the wing on an aircraft isn’t moving at all and as we move out beneath the wing or above it, the air flow speeds up until eventually it matches the airspeed of the aircraft.
In laminar flow the air moves in “tubes” that don’t cross each other. Each streamline contains a column of fluid that doesn’t “talk” to the other columns of fluid. This is what the streamlines, shown in the diagram below, mean. They designate areas of flow that are independent from each other. Slipstreams don’t collide unless you’re in turbulent flow.
Under normal flight, the airflow across an aircraft is for the most part laminar. There are exceptions, such as at the wing tips, where vortices develop but that’s beyond this discussion of lift1.
The effect of this is that the wing bends the air around the wing. It’s this bending that produces the lift. The diagram below illustrates this:

You can see that after the air leaves the trailing edge of the wing it still traveling downwards following Newton’s first law. This is the mechanism by which a large amount of air is accelerated around the wing to produce lift.
Conclusion
In this post we’ve seen how the explanation of lift given by Bernoulli’s formula is an incorrect theory of lift. It makes the wrong predictions about the properties of a wing.
Under Newtonian lift it is obvious why a wing produces more lift at a higher angle of attack. Under Bernoulli this is not possible.
Newtonian lift tells us why a plane can fly upside down and maintain height. Bernoulli’s lift is powerless to explain this.
This is probably one of the most popular incorrect theories taught in the science class room. What’s more is that it is actually more difficult to grasp the Bernoulli theory than it is to grasp the Newtonian one.
It is anyone’s guess why the myth of Bernoulli’s effect producing the wing’s lift is so persistent!
-
They become important in understanding ground effect, where much more lift is produced when the plane is less than one wingspan above the ground. ↩